21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234Example 1 In the integral we may write = , = , = , so that the integral becomes = = ( ) = = = = , provided For a definite integral, the bounds change once the substitution is performed and are determined using the equation = , with values in the range <

Graham S Formula For Determinant Of Distance Matrix Of A Tree Mathematics Stack Exchange
2^0+2^1+...+2^n-1 formula
2^0+2^1+...+2^n-1 formula-≥2% in H 2 O, ≥90 atom % 17 O Pricing Match Criteria Keyword Hydrogen peroxide 35% Hydrogen peroxide 35% Synonyms Hydrogen peroxide solution CAS Number Molecular Weight 3401 Beilstein Registry NumberTwo numbers r and s sum up to 5 exactly when the average of the two numbers is \frac{1}{2}*5 = \frac{5}{2} You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC



2 2 Some Summation Formulas
It's not It's actually 1 (2)^3=8 (2)^2=4 (2)^1=2 There seems to be a pattern here Every time the exponents goes down 1, the answer is divided by 2 So, by this logic, if you take away from from the exponent 2^1, you get 2^0, and you applThe modulo (%) operator calculates the remainder of a division operation In this case, it calculates the remainder of i divided by 2If i is an even number, the result will be 0 and if it is an odd number, the result will be 1So this if statement checks to see if i is an even number If A = (1 2 0), (2 1 2), (0 1 1), find A1 Using A–1, solve the system of linear equations x – 2y = 10 , 2x – y – z = 8 , –2y z = 7
Formula contains the expression You still use the formula to find the width of the trapezoids The coefficients in the Trapezoidal Rule follow the pattern 1 2 2 2 2 2 1 The Trapezoidal Rule A Second Glimpse where a, b is partitioned into n subintervals of equal length If we plug 6 into our equation, the result is 127 2^ (6 1) 1 = 127 If we manually add the powers of 2^6, the result is also 127 1 2 4 8 16 32 64 = 127 💥 Proof! definition is —used postpositively to describe a new and improved version or example of something or someone How to use in a sentence
Inductive Step to prove is $ 2^{n1} = 2^{n2} 1$ Our hypothesis is $2^n = 2^{n1} 1$ Here is where I'm getting off track Lets look at the right side of the last equation $2^{n1} 1$ I can rewrite this as the following $2^1(2^n) 1$ But, from our hypothesis $2^n = 2^{n1} 1$ Thus $2^1(2^{n1} 1) 1$ This is where I get lostSolve Quadratic Equation by Completing The Square 22 Solving n22n1 = 0 by Completing The Square Add 1 to both side of the equation n22n = 1 Now the clever bit Take the coefficient of n , which is 2 , divide by two, giving 1 , and finally square it Hello Mr Jain, Kindly find the below formulas for calculating sample size based on your inputs For continuous data N= (Z*S/E)^2 N Sample size Z – Constant for confidence level (like 1645 90%, 196 95%, 2575 99%) S Standard deviation



1




Wallis Product Wikipedia
For example 3 (−2) = 3−2 = 1 Knowing this, let us try an example Example 3 Find the mean of these numbers 3, −7, 5, 13, −2 The sum of these numbers is 3 − 7 5 13 − 2 = 12 ;Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for This makes absolutely no sense I mean, look at it for a second firstly you failed to notice the pattern correctly since 2^n means 2^12^22^3 instead of what is shown And secondly, how can that all equal 2^(n1) when on the left side of the equation, you already have 2^n which means the term just before the last is 2^(n1)?




Prep05sols Preparation For Tutorial Math1005 Answers To Question Set For B2 Sequences Page Of Throughout These Questions The Notation Will Be Used As Studocu




Discrete Mathematics Prezentaciya Onlajn
$\tag 1 n^2 = (n 1)^2 2 (n 1) 1$ Observe that the first term of the rhs of $\text{(1)}$ is the square of an integer, just like the lhs of $\text{(1)}$ So you can use 'downward finite induction formula recursion' (not sure what to call this) and conclude thatThere are 5 numbers The mean is equal to 12 ÷ 5 = 24;The sum of the first n squares, 1 2 2 2 n2 = n ( n 1) (2 n 1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes from Instead we




Graham S Formula For Determinant Of Distance Matrix Of A Tree Mathematics Stack Exchange



1
32 Solving n2n2 = 0 by Completing The Square Add 2 to both side of the equation n2n = 2 Now the clever bit Take the coefficient of n , which is 1 , divide by two, giving 1/2 , and finally square it giving 1/4 Add 1/4 to both sides of the equation On the right hand side we have 2 1/4 or, (2/1I have wondered how the closed form for the sum of squares for the first n natural numbers was derived Given the formula for the sum 1^22^2n^2= n(n1)(2n1)/6 I learned to prove its correctness using mathematical induction However, I neverCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Pdf Math 104 Summer 06 Homework 1 Solution Joohong Kim Academia Edu




Math 55 Discrete Mathematics Pdf Free Download
Fibonacci Sequence A Fibonacci sequence is a sequence in which every number following the first two is the sum of the two preceding numbers The first two numbers in a Fibonacci sequence are defined as either 1 and 1, or 0 and 1 depending on the chosen starting point4 Probability 9 Let W 1 and W 2 be independent discrete random variables, each having the probability function given by f(0) = 1 2, f(1) = 1 3, and f(2) = 1 6 Set Y = W 1 W 2 (a) Determine the mean, variance, and standard deviation of Y That will give the same value in each cell though, whereas is b=1 and N= 4 the values should be 2, 15, 1, 05, 0, 0,5, 1, 15, 2 – user Jan 13 '14 at 1507 have you pressed CTRLSHIFTENTER to evaluate the formula or just ENTER ?



Example Of 2d Convolution



Addupsequences
@Stephan, that's the formula if the N is added on the left side If it's not, one N is missing, so 2N should be subtracted in the numerator – Johannes Schaub litb Mar '10 at 1716 Explanation Matrix A characteristic polynomial is p(λ) = 1 − 3λ 3λ2 −λ3 = −(λ −1)3 and A obeys this characteristic equation so A3 = 3 −3A I There is a difference equation associated to this relationship an3 = 3an2 − 3an1 an The difference equation solution is an = C0 nC1 n2C2 so finallyGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



2 2 Some Summation Formulas



Http Faculty Washington Edu Eathomp Stat394 08 Notes Week2 Pdf
Simple and best practice solution for n/1=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, Explanation using the method of proof by induction this involves the following steps ∙ prove true for some value, say n = 1 ∙ assume the result is true for n = k ∙ prove true for n = k 1 n = 1 → LH S = 12 = 1 and RHS = 1 6 (1 1)(2 1) = 1 ⇒result is true for n = 1F (2) = (2) 2 2(2) – 1 To keep things straight in my head (and clear in my working), I've put parentheses around every instance of the argument 2 in the formula for f Now I can simplify
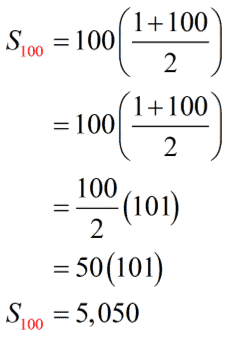



Arithmetic Series Formula Chilimath



Solved Problem 3 Suppose We Have Two Four Point Sequences R N And H N As Follows X N Cos 2 N 0 1 2 3 H N 2 Quot N 0 1 2 3 I Cal Course Hero
2 n1 – 2 = 2 11 – 2 = 2 2 – 2 = 4 – 2 = 2 So (*) works for n = 1 In the "n = k 1" step, it is usually a good first step to write out the whole formula in terms of k 1, and then break off the "n = k" part, so youSum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 442 Solving 2n 2n1 = 0 by Completing The Square Divide both sides of the equation by 2 to have 1 as the coefficient of the first term n 2(1/2)n(1/2) = 0 Add 1/2 to both side of the equation n 2(1/2)n = 1/2 Now the clever bit Take the coefficient of n , which is 1/2 , divide by two, giving 1/4 , and finally square it giving 1/16




M3u1d3 Warm Up 12 6 0 6 4 4 3 4 9 4 27 2 5 8 11 14 0 2 6 12 Arithmetic An An Geometric An A1 1 2 N Ppt Video Online Download




Solve The Recurrence Relation A N 12a N 2 Chegg Com
(1) we will prove that the statement must be true for n = k 1Of the formulas for Bk¡1 and Bk¡2 we get Bk = Bk¡1 6Bk¡2 (1) 2¢3 k¡1(¡1)(¡2) 6 £ 2¢3k¡2 (¡1)(¡2)k¡2 (2) = 2(36)3k¡2 (¡1)(¡26)(¡2)k¡2 (3) = 2¢3 2¢3k¡ (¡1)¢(¡2)2 ¢(¡2)k¡2 (4) = 2¢3k (¡1)(¡2)k (5) Thus the formula holds for k, contradicting the assumption that k is the smallest number for which the formula fails So there can be no such number the formula'Clearly a David would fly fewer immediate red flags for a human trying to love him than David' 'As I told you guys in my interview, this is a revolution ' 'Zwan is kind of like Smashing Pumpkins ' 'If current fiscal deficits had not been allowed to unfold, the Great Recession would now be Great Depression '
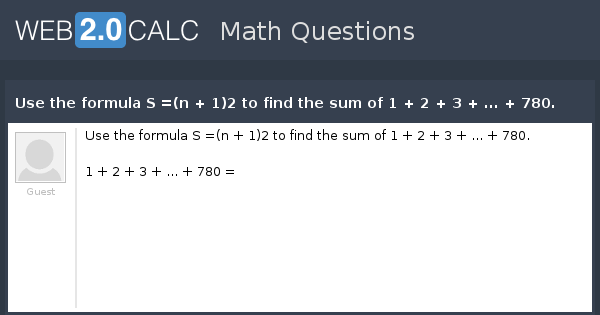



View Question Use The Formula S N 1 2 To Find The Sum Of 1 2 3 780



What Is The Value Of 1 2 2 2 3 2 N 2 Quora
Answers and Replies Your solution is fine, but your presentation is hard to follow As you know, you need to prove that 2 0 = 2 1 − 1 and then that if 1 ⋯ 2 k = 2 k 1 − 1 then 2 0 ⋯ 2 k 1 = 2 k 2 − 1 To prove the former, I would just write 2 0 = 1 = 2 1 − 1 The calculation that proves the latter is much easier toWhen n = 1 the left side has only one term, 2 n1 = 2 11 = 2 0 = 1 The right side is 2 n 1= 2 1 1 = 1 Thus the statement is true for n = 1 The second step is the inductive step You need to show that if the statement is true for any particular value of n it is also true for the next value of n If you can do this then, since it is trueThe sum of the powers of two is one less than the product of the next power Don't take my word for it Try it with a larger value



2




X2 N 1x N 2 0 Gauthmath
\begin{aligned} \frac { \sum _{ i=1 }^{ 17 }{ { i }^{ 2 } } }{ 1009\cdot 1345 } &=\frac {\ \ \frac { 17(171)(2\cdot 171) }{ 3!Empirical Formula (Hill Notation) H 2 17 O 2 Product Number Product Description SDS;Simplify (2^ (n1))/ ( (2^n)^ (n1)) 2n1 (2n)n−1 2 n 1 ( 2 n) n 1 Reduce the expression by cancelling the common factors Tap for more steps Multiply the exponents in ( 2 n) n − 1 ( 2 n) n 1 Tap for more steps Apply the power rule and multiply exponents, ( a m) n




n2 Formula




How To Derive N 1 2 From 1 2 3 N N Quora
Osmolite ® 12 Cal Complete, Balanced Nutrition® without Fiber OSMOLITE 12 CAL is highprotein therapeutic nutrition that provides complete, balanced nutrition for long or shortterm tube feeding for patients who may benefit from increased protein and calories}\ \ }{ 1009\cdot 1345 } \\ \\ &=\frac {\ \ \frac { 17\cdot 18\cdot 4035 }{ 2\cdot 3 }\ \ }{ 1009\cdot 1345 } \\\\ &=\frac { 17\cdot 1009\cdot 1345 }{ 1009\cdot 1345 } \\ \\ &=17\ _\square \endMolecular Weight Empirical Formula (Hill Notation) C15H13N3S Product Number Product Description SDS 1497 A cellpermeable autophagy inducer that selectively induces nonapoptotic cell death in VHLdeficient, but not VHLexpressing, renal carcinoma cells both in vitro and in mice in vivo



Untitled Document



Solved Consider The Equation O 2 Un 1 2 Un 2n 1 H 2n For N 1 2 3 Course Hero
Therefore we subtract off the first two terms, giving ∞ ∑ n = 2(3 4)n = 4 − 1 − 3 4 = 9 4 This is illustrated in Figure Since r = 1 / 2 < 1, this series converges, and by Theorem 60, ∞ ∑ n = 0(− 1 2)n = 1 1 − ( − 1 / 2) = 2 3 The partial sums of this series are plotted in Figure (a)The LCM of 1, 1, 2 1, 1, 2 is the result of multiplying all prime factors the greatest number of times they occur in either number 2 2 The factors for n 2 n 2 are n ⋅ n n ⋅ n, which is n n multiplied by each other 2 2 times n 2 = n ⋅ n n 2 = n ⋅ n n n occurs 2 2 times The factor for n 1 n 1 is n n itselfThe partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was known




For Each Of The Following Functions F With Domain N Chegg Com




2 Write A Formula For The Px13n Term For Each S Gauthmath
In Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to 12 = 1 2 3 6 and is obviously true Assuming the statement is true for n = k 12 22 32 k2 = k(k 1)(2k 1) 6;All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2x1=0 x 2 2 x − 1 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 1 for c Given an integer N, the task is to find the sum of series 2 0 2 1 2 2 2 3 2 n Examples Input 5 Output 31 2 0 2 1 2 2 2 3 2 4 = 1 2 4 8




A Verify The Reduction Formula For N Chegg Com




6 A The Formula For The N Th Term Of The Sequence 2
1 2 4 8 ⋯ The first four partial sums of 1 2 4 8 ⋯ In mathematics, 1 2 4 8 ⋯ is the infinite series whose terms are the successive powers of two As a geometric series, it is characterized by its first term, 1, and its common ratio, 2Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots



2
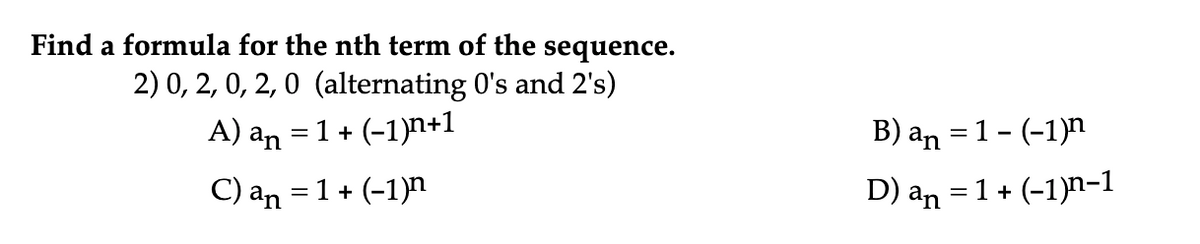



Answered Find A Formula For The Nth Term Of The Bartleby
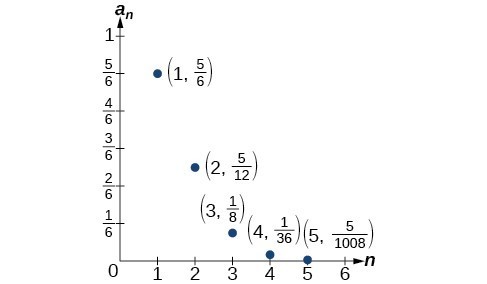



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra
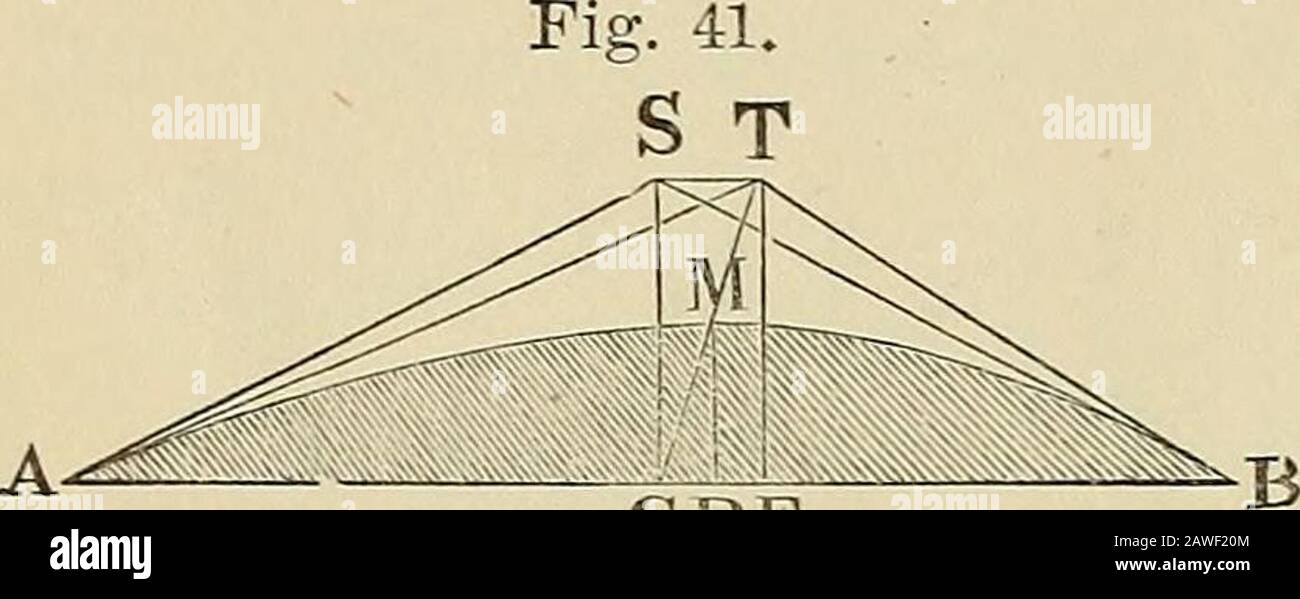



Elements Of Analysis As Applied To The Mechanics Of Engineering And Machinery Troduce These Values Into The Formula Ydx J O 8x 2 0 2 N 4 2 1




Math 257 316 Assignment 2 Solutions




n2 Formula Proof




Chapter 1



3



2




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange



2




Otjwkhfxsa7skm




Use The Binomial Formula 1 Alpha N 1 N Alpha Chegg Com




Geometric Series Wikipedia



Mathfunc



1
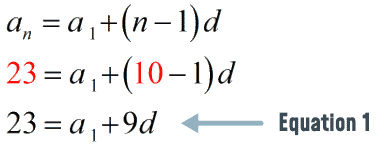



Arithmetic Series Formula Chilimath



How To Get The Sum Of 1 2 3 4 5 6 N In C Language Using A Function Quora




Ece 250 Algorithms And Data Structures Mathematical Background



Web Northeastern Edu Suciu Mth1125 1125sp02 Sol3 Pdf




Median Formula In Statistics Examples Meaning Mean Mode




How To Prove A Formula For The Sum Of Powers Of 2 By Induction Mathematics Stack Exchange
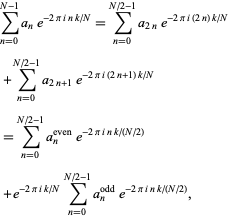



Fast Fourier Transform From Wolfram Mathworld




Find A Formula For The Nth Term Of The Sequence 0 Chegg Com



Untitled Document




1 Recurrence 1 Sequence 2 Recursively Defined Sequence 3 Finding An Explicit Formula For Recurrence Relation Ppt Download



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




Discrete Mathematics Online Presentation



Solved 7 1 2 3 Points Previous Answershunterdmz 3 2 006 Consider The Following Recurrence Relation 4 Ifn 0 Q N Z Q N 1 3ifn 0 Prove By Course Hero




Geometric Series Wikipedia




Just Need Help Finding The A 3 N General Formula Chegg Com




Answered Hence A Player S Probability Of Winning Bartleby




Please Show All The Step 3 Find The Standard Deviation Of The Data Set 1 2 3 4 5 Using Homeworklib




What Is The Explicit Formula Represented By This Graph A An 1 1 N 1 B An 1 1 N 1 C Brainly Com




Sequences Linear Quadratic Demonstration Ppt Download




Write Down A Main And A Function To The Following Or Home Work




Solved Write Non Recurrent Formula Sequence Beginning 1 3



Solved 7 3 3 Points Previous Answershunterdmz 3 2 006 Consider The Following Recurrence Relation 4 Ifn 0 N Q 2 Q N 1 3 Ifn 0 Prove By Course Hero




What Is The Sum Of The First 50 Terms Of A Sequence Of 1 3 5 7 And 9 Quora




Solved A Use The Reduction Formula In Example 6




Pdf Bethe Equation At Q 0 Moebius Inversion Formula And Weight Multiplicities Ii X N Case Semantic Scholar




Pdf Important Sum Formulas Omid Motahed Academia Edu



Mathfunc




2x Lt 1 X 2n 1x



2



Http Www Matthewkahle Org Download File Fid 561



Http Www Marywood Edu Math Challenge Problems Powsol Pdf




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange




Geometric Sequences And Sums




Ch 12 Study Guide Do Not Write On
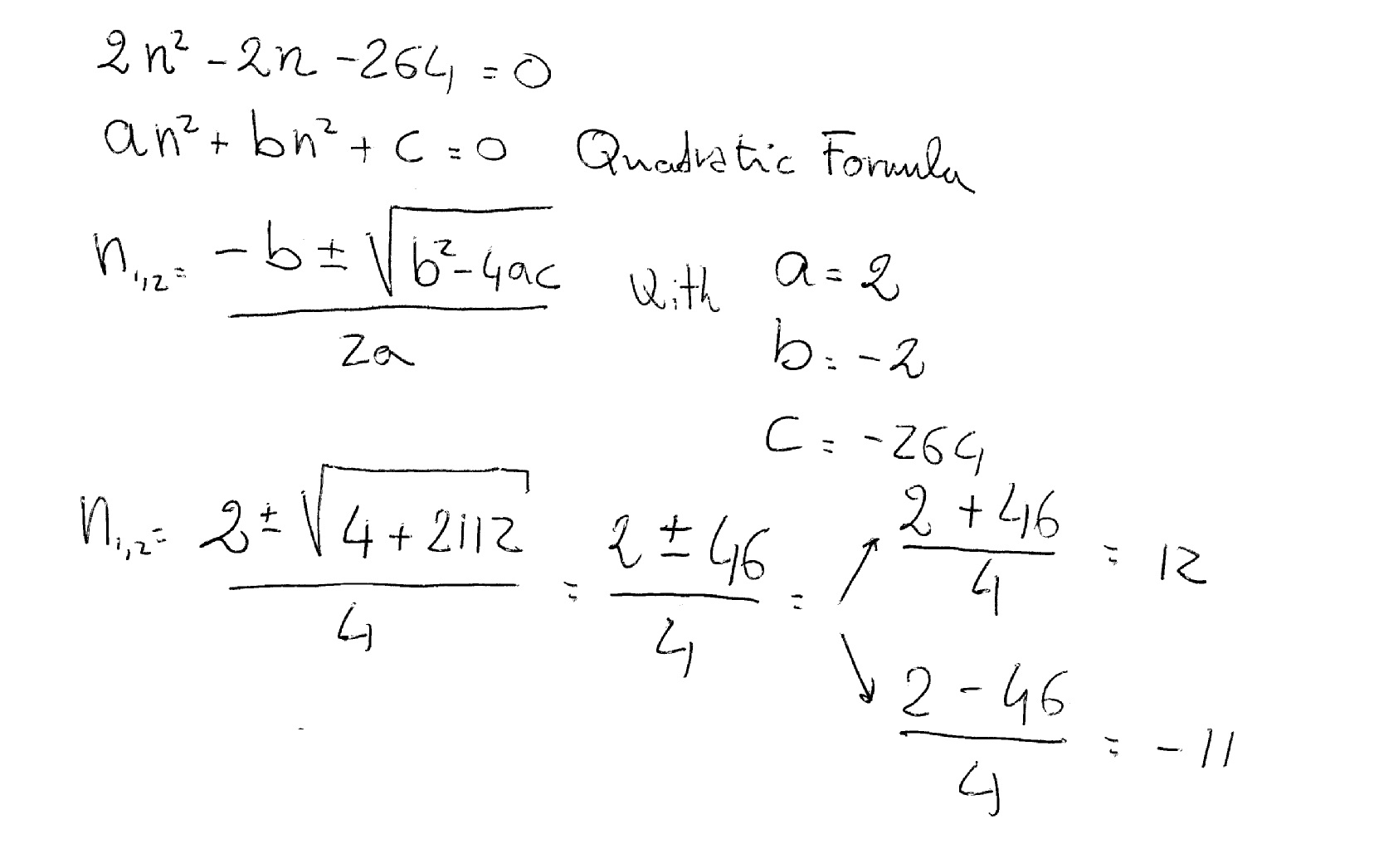



How Do You Find The Solution To The Quadratic Equation 2n 2 2n 264 0 Socratic




Find A Formula For The Nth Term Of The Sequence 0 Chegg Com




Geometric Series Wikipedia




Discrete Math 30 Final Test 4 Review Ch 5 Only Highlighted Items Flashcards Quizlet




Legendre Polynomials Rodrigues Formula And Recursions



2



Http Pages Uoregon Edu Ddugger Ma307 Hw9sol Pdf




Sequences And Summations Cs 2 Epp Section 4



Http Math Ksu Edu Gerald Math510 Hw13 Pdf




1234n Formula




Recursion



Http People Math Harvard Edu Knill Teaching Math464 1997 Math464 565 1997 Pdf




Pdf Compactly Generating All Satisfying Truth Assignments Of A Horn Formula
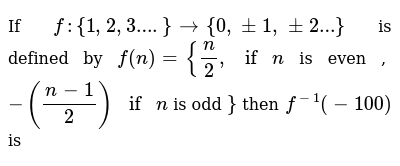



If F 1 2 3 Gt 0 1 2 Is Defined By F N N 2




B Let T 2 N R Da Sin Use The Reduction Formula To Chegg Com
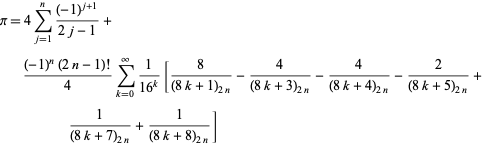



Pi Formulas From Wolfram Mathworld




n2 Formula




Pdf A Simple Form For Coefficients In A Family Of Ordinary Differential Equations Related To The Generating Function Of The Legendre Polynomials




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 19 Arithmetic Progressions Download Free Pdf




Prove That 1 3 2 3 3 3 N 3 N N 1 2 2 Teachoo




Mth3101 Advanced Calculus Chapter 2




Solve The Recurrence Relation S 1 0 S N 2s N 2 N Using The Formula C N 1 Homeworklib
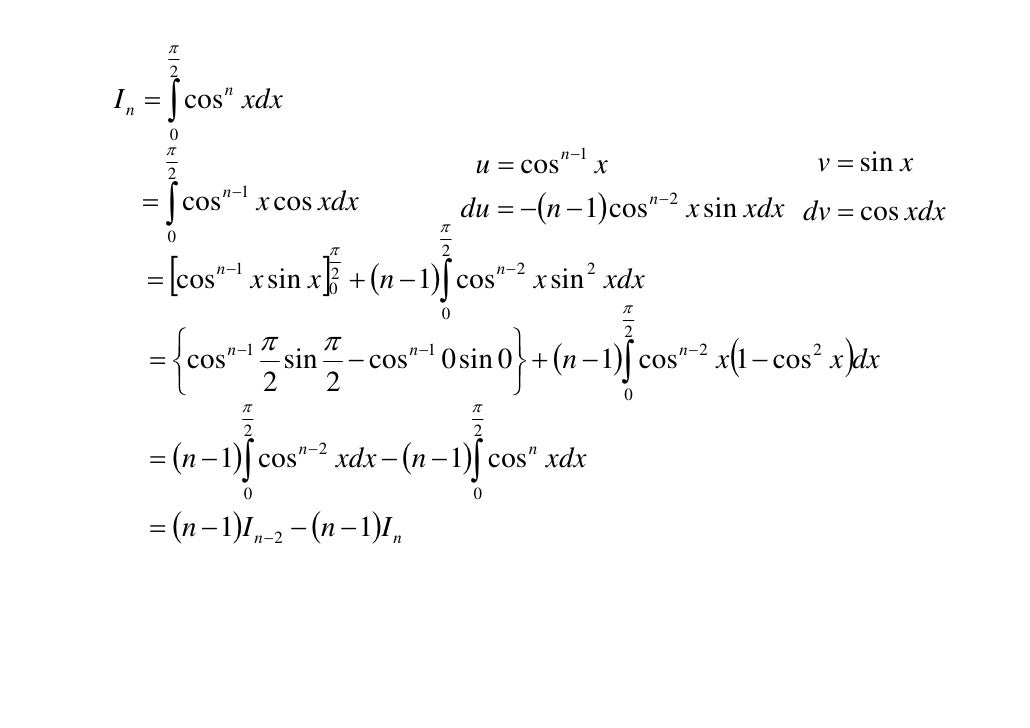



Otjwkhfxsa7skm




Graphing Parabolas



Http Www Math Drexel Edu Dmitryk Teaching Math221 Spring 12 Quiz4 Solutions Pdf




Induction And Recursion By Mohsin Tahir Gl Numan Ul Haq Waqas Akram Rao Arslan Ali Asghar Ppt Download


